Most important among the features of a debugger is the ability to display values of objects from the target program. This operation is generically called expression evaluation, even though, as we shall see, expression evaluation may involve many other operations than simply displaying the value contained in some memory location.
We'll start discussing the basic concepts, and then we'll evolve the discussion to include the most difficult expressions. A lot of this material is directly related to compiler theory, although using such principles in a debugger requires special considerations.
We'll attack the problem of expression evaluation by splitting it into 3 phases:
- expression parsing;
- location evaluation;
- value computation.
Expression parsing
Expression parsing in the context of a debugger usually means to try to reproduce the same behavior that the high-level language defines for a given language.
Consider the following expression:
2 + 5 * 7
In C, and many other languages, it evaluates to 37. This is because the * operation has a higher priority than the + operator. This can be represented by the following tree:
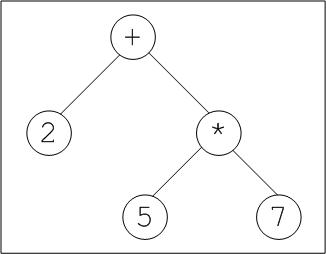
The task of the parser is to construct such trees for a given input string.
Even when an expression includes more complex operators, the main issue is usually to construct a tree that follows the conventions set up by the high-level language.
In this sense there is not much difference with a C parser used in a compiler front-end.
Location Evaluation
An expression with only constants can be easily evaluated by a recursive traversal of the tree. When an expression involves program variables, however, it's possible that the debugger will have to access the target to retrieve the value of the variable from the location where the variable is allocated.
For example, the following expression:
local1 + global_arr [ index ]
may involve at least 3 accesses to the target memory, to retrieve the values "local1", "index", and "global_arr[index]". There may be more target accesses involved if the location of "local1" or "index" is not known at compile time but it must be computed by the debugger.
One task of the expession evaluator is to convert such nodes into the corresponding location on the target.
In case of terminal nodes, the information usually comes from the Symbol Table. A named symbol is looked up in the current context in the SymbolTable. If the Symbol is found, then one of its locations is retrieved and used in place of the name of the symbol.
For example, the above expression could be converted into the following pseudo-code:
SP[-8] + *(0x140020 + R3 * 4)
where:
- SP[-8] is the location of "local1";
- 0x140020 is the address of the first byte of "global_arr";
- R3 is the location of "index"
We have omitted the size of each access. This also comes from the symbolic information for each symbol. If, for example, "global_arr" is an array of shorts, "index" will have to be multiplied by 2, and an appropriate sign-extension will have to be performed before adding the retrieved value to "local1".
We can traverse the tree and replace symbolic references with nodes that represent the actual locations of the variables. This does not require accesses to the target, and can be performed using a recursive traversal of the initial tree.
We should note that location evaluation depends on the current context. A context is the set of registers that identifies the current stack frame. Typically, most evaluations will use the actual values contained in the processor registers.
However, if the user has focused the debugger on a previous stack level, the location of local variables has to be computed relative to that stack level. The stack frame detector is in charge or presenting to the expression evaluator with the set of values for each registers belonging to a particular stack level.
The location evaluator can ask the stack frame detector to return the actual location of each register for the desired stack level, and use that location in place of the actual register name.
Say for example that we are examining the stack 2 levels up the most active function. We could then rewrite the above sample expression using the following pseudo-code:
SP[+0x50] + *(0x140020 + SP[+0x64] * 4)
where SP[+0x50] is the location of "local1" and SP[+0x64] is the location when R3 has been saved by the intervening function calls prologue code.
Value Computation
Once we have the location of all variables, it is possible to read each variable's value as we encounter its node during the recursive traversal of the tree. The following pseudo-code shows how to implement a recursive traversal of the expression tree:
bool Evaluate(Node *tree, Result& result)
{
Result leftResult, rightResult;
if(tree->m_left)
if(Evaluate(tree->m_left, leftResult)
== false)
return false;
if(tree->m_right)
if(Evaluate(tree->m_right,
rightResult) == false)
return false;
switch(tree->m_oper) {
case OP_ADD:
result.m_val = leftResult.m_val +
rightResult.m_val;
return true;
case OP_MULT:
result.m_val = leftResult.m_val * rightResult.m_val;
return true;
...
case OP_SYMBOL:
ReadMemory(tree->m_location, result);
return true;
}
return false;
}
This approach has the following drawbacks:
- One has to wait for the target to return the value of each variable. This may take a long time, if the connection to the target is slow, or it may even hang if the target is not responding. Killing such operation while there are active debugger stack frames is difficult, since each active function has to be cleanly removed from the stack. C++ allows the use of try / catch clauses; these usually complicate coding, since one has to know which exception is likely to be thrown, in addition to other complications that we'll consider later, when the expression evaluator has to interact with the execution engine.
- One has to return error codes when the expression doesn't make sense, for example because some identifier does not match the requested operation (for example when a non-pointer is used to access a structure or an array).
- Recursive evaluation can use a lot of stack space. Stack space is limited on individual threads of execution. Only the main thread has an "unlimited" stack, and we'll see that using a recursive evaluator requires the use of multiple threads, thus imposing a limitation on the amount of stack available for the recursion.
The alternative to a recursive traversal of the tree nodes is the use of a non-recursive evaluator. This has several advantages, including the possibility of aborting the evaluation at any time, regardless of how many nodes have been evaluated so far. This makes it very easy for the GUI to stop evaluation of expressions when the user decides to issue another command without waiting for the result of the expressions.
The following pseudo-code shows how to convert the previous recursive evaluator code into a non-recursive evaluator:
EvalStack nodeStack;
ResultStack results;
bool Evaluate(Node *tree, Result& result)
{
Result *leftResult, *rightResult;
Node *n;
nodeStack.Push(tree, EVAL_INIT);
while(nodeStack.Length() > 0) {
EvalState *current = nodeStack.Pop();
n = current->m_node;
switch(current->m_state) {
case EVAL_INIT:
if(n->m_left)
{
current->m_state = EVAL_RIGHT;
nodeStack.Push(current);
nodeStack.Push(n->m_left, EVAL_INIT);
continue;
}
// evaluate
leaf node,
// such as
numeric constants
switch(n->m_oper)
{
case
OP_VALUE:
result.m_value = n->m_value;
break;
case
OP_SYMBOL:
TaskReadMem *task = new TaskReadMem();
nodeStack.Push(task, EVAL_MEMORY);
break;
...
}
results.Push(result);
continue;
case EVAL_MEMORY:
TaskReadMem
*task = current->m_task;
result.m_value = task->m_value;
delete task;
results.Push(result);
// fall
through to next case
case EVAL_RIGHT:
if(n->m_right)
{
current->m_state = EVAL_BINARY;
nodeStack.Push(current);
nodeStack.Push(n->m_right, EVAL_INIT);
continue;
}
// evaluate
unary operators.
// Unary
operators don't have right descendants
leftResult =
results.Pop();
switch(n->m_oper)
{
case OP_NOT:
leftResult->m_value = !leftResult->m_value;
break;
...
}
results.Push(leftResult);
continue;
case EVAL_BINARY:
leftResult =
results.Pop();
rightResult =
results.Pop();
switch(n->m_oper)
{
case OP_ADD:
leftResult->m_value +=
rightResult->m_value;
break;
...
}
results.Push(leftResult);
continue;
}
}
}
The advantage of this code is that the user can decide to cancel any Task that is pending, such as the TaskReadMemory above, without worrying about having to unwind the stack of active function calls. Simply deleting all entries in the nodeStack and results stacks will reclaim any memory used by the evaluator with no need of try / catch, multiple threads, semaphores etc.
This approach makes it very easy to solve another difficult problem: the interaction between the expression evaluator and the execution engine.
In one possible scenario, the execution engine runs the target code until a breakpoint is reached. At that point the debugger reports to the user that execution has stopped.
However, an expression may be associated with the breakpoint, to indicate that execution should stop only when the expression evaluates to true.
In this case, the execution engine must ask the expression evaluator to compute the value of the expression, and based on the value it must decide whether to continue execution of the target program.
We could think that the execution engine could simply call the expression evaluator and wait for it to compute the result. However, if the user decides to force stopping the target by hitting Ctrl-C (or any other means the GUI uses to stop execution), the debugger now has to stop not only the evaluation of the expression, but also tell the execution engine that it should not continue the target program regardless of the result of the evaluation.
Using the Task architecture this is simple to achieve: we just record in both the TaskContinue and the TaskEval objects that the user has aborted the operation, and let the TaskManager clean up the memory associated with the two Tasks. There is no need to clean up active functions on the debugger's stack, no need to make sure that the state of internal debugger tables is consistent, no need to synchronize with multiple threads of execution.
Another benefit is achieved when the expression to evaluate involves target function calls. Expressions such as the following one require calling a target function:
strcmp(a, "myString") == 0
In this case, it is the expression evaluator that has to call the execution engine and has to wait for execution of the strcmp() function to finish before resuming the evaluation of the expression. Again, using a non-recursive evaluator and a single thread of execution eliminates all possible problems caused by the execution engine holding a lock to prevent recursive or concurrent execution of its critical regions.
Hopefully this discussion has made a good case for the use of Task objects and the use of a non-recursive evaluator in a debugger. Implementing the code using these principles will show even more that what are usually complex problems in these two central pieces of the debugger are solved easily and naturally.
© 2007 Giampiero Caprino, Backer Street Software